Fitting distributions using primarycensored and fitdistrplus

1 Introduction

1.1 What are we going to do in this vignette

In this vignette, we’ll demonstrate how to use primarycensored in conjunction with fitdistrplus for fitting distributions. We’ll cover the following key points:

Simulating censored delay distribution data
Fitting a naive model using fitdistrplus
Evaluating the naive model’s performance
Fitting an improved model using primarycensored functionality
Comparing the primarycensored model’s performance to the naive model

1.2 What you will learn

By the end of this vignette, you will be able to: - Understand the bias introduced by ignoring primary censoring and truncation when fitting delay distributions - Use fitdistdoublecens() to fit distributions that properly account for primary censoring, secondary censoring, and truncation - Understand when MLE-based fitting with fitdistrplus is appropriate versus Bayesian approaches with Stan

1.3 What might I need to know before starting

This vignette assumes some familiarity with the fitdistrplus package. If you are not familiar with it then you might want to start with the Introduction to fitdistrplus vignette.

1.4 How does this vignette differ from fitting distributions with Stan vignette

This vignette is similar to the vignette("fitting-dists-with-stan") vignette in that it shows how to fit a distribution using primarycensored. However, here we use maximum likelihood estimation (MLE) to fit the distribution, rather than MCMC. In some settings this may result in a faster fit, but in other settings especially when the data is complex, MCMC may be more reliable. The major benefit of the fitdistrplus approach is that we don’t need to install additional software (Stan) to fit the distribution. Note that rather than returning credible intervals, the fitdistrplus package returns standard errors and confidence intervals.

1.5 Packages used in this vignette

Alongside the primarycensored package we will use the fitdistrplus package for fitting distributions. We will also use the ggplot2 package for plotting and dplyr for data manipulation.

library(primarycensored)
library(fitdistrplus)
library(ggplot2)
library(dplyr)

2 Simulating censored and truncated delay distribution data

We’ll start by simulating some censored and truncated delay distribution data. We’ll use the rprimarycensored function (actually we will use the rpcens alias for brevity).

set.seed(123) # For reproducibility

# Define the number of samples to generate
n <- 1000

# Define the true distribution parameters
shape <- 1.77 # This gives a mean of 4 and sd of 3 for a gamma distribution
rate <- 0.44

# Generate fixed pwindow, swindow, and obs_time
pwindows <- rep(1, n)
swindows <- rep(1, n)
obs_times <- sample(8:10, n, replace = TRUE)

# Function to generate a single sample
generate_sample <- function(pwindow, swindow, obs_time) {
  rpcens(
    1, rgamma,
    shape = shape, rate = rate,
    pwindow = pwindow, swindow = swindow, D = obs_time
  )
}

# Generate samples
samples <- mapply(generate_sample, pwindows, swindows, obs_times)

# Create initial data frame
delay_data <- data.frame(
  delay = samples,
  delay_upper = samples + swindows,
  pwindow = pwindows,
  relative_obs_time = obs_times
)

head(delay_data)

##   delay delay_upper pwindow relative_obs_time
## 1     2           3       1                10
## 2     1           2       1                10
## 3     2           3       1                10
## 4     4           5       1                 9
## 5     3           4       1                10
## 6     4           5       1                 9

# Compare the samples with and without secondary censoring to the true
# distribution
# Calculate empirical CDF
empirical_cdf <- ecdf(samples)

# Create a sequence of x values for the theoretical CDF
x_seq <- seq(0, 10, length.out = 100)

# Calculate theoretical CDF
theoretical_cdf <- pgamma(x_seq, shape = shape, rate = rate)

# Create a long format data frame for plotting
cdf_data <- data.frame(
  x = rep(x_seq, 2),
  probability = c(empirical_cdf(x_seq), theoretical_cdf),
  type = rep(c("Observed", "Theoretical"), each = length(x_seq)),
  stringsAsFactors = FALSE
)

# Plot
ggplot(cdf_data, aes(x = x, y = probability, color = type)) +
  geom_step(linewidth = 1) +
  scale_color_manual(
    values = c(Observed = "#4292C6", Theoretical = "#252525")
  ) +
  geom_vline(
    aes(xintercept = mean(samples), color = "Observed"),
    linetype = "dashed", linewidth = 1
  ) +
  geom_vline(
    aes(xintercept = shape / rate, color = "Theoretical"),
    linetype = "dashed", linewidth = 1
  ) +
  labs(
    title = "Comparison of Observed vs Theoretical CDF",
    x = "Delay",
    y = "Cumulative Probability",
    color = "CDF Type"
  ) +
  theme_minimal() +
  theme(
    panel.grid.minor = element_blank(),
    plot.title = element_text(hjust = 0.5),
    legend.position = "bottom"
  ) +
  coord_cartesian(xlim = c(0, 10)) # Set x-axis limit to match truncation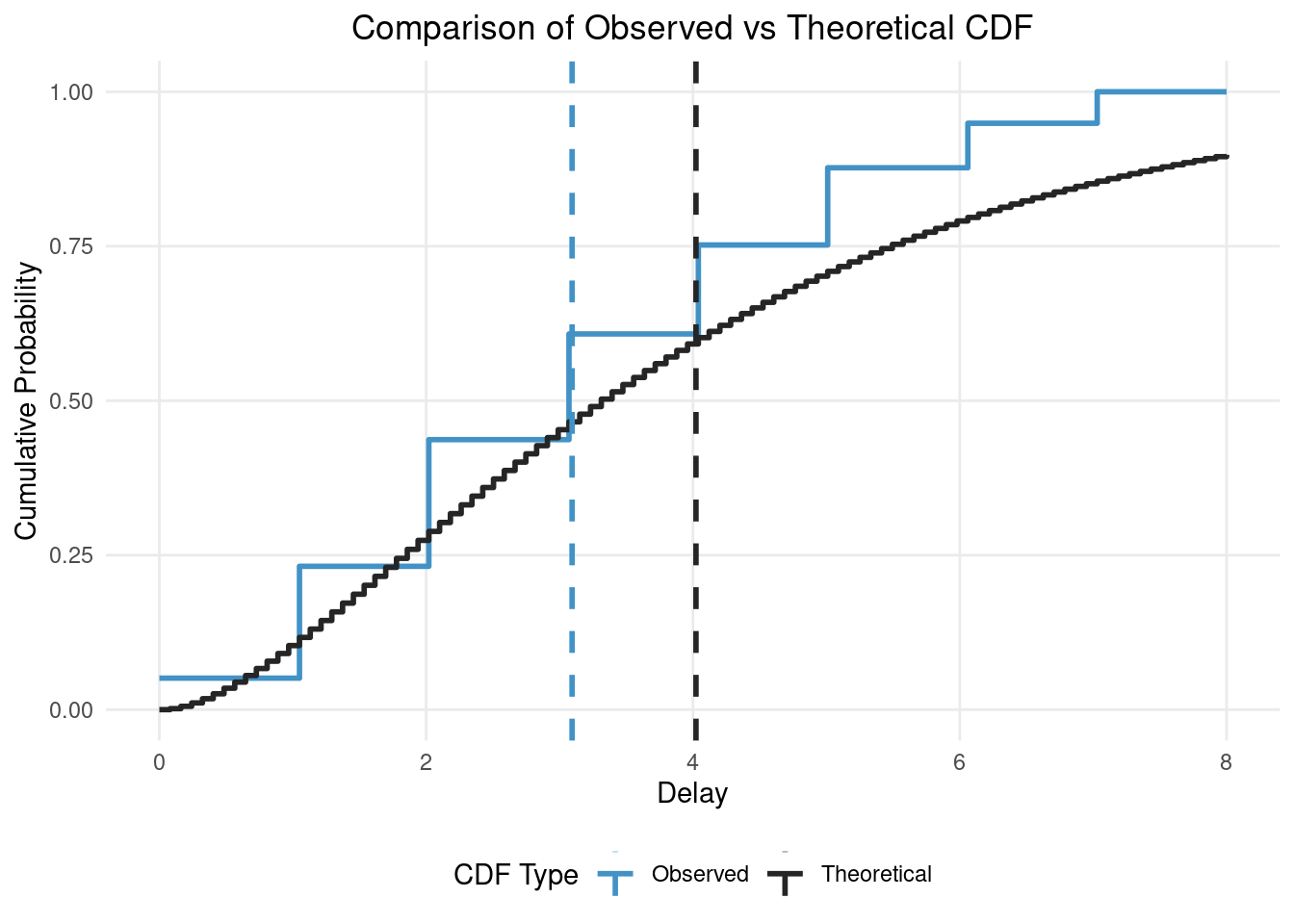

In this figure you can see the impact of truncation and censoring as the observed distribution has a much lower mean (the vertical dashed blue line) than the true/theoretical distribution (the vertical dashed black line). Our modelling aim is to recover the true parameters of the theoretical distribution from the observed distribution (i.e. recover the black lines from the blue lines).

3 Fitting a naive model using `fitdistrplus`

We first fit a naive model using the fitdistcens() function. This function is designed to handle secondary censored data but does not handle primary censoring or truncation without extension.

fit <- delay_data |>
  dplyr::select(left = delay, right = delay_upper) |>
  fitdistcens(
    distr = "gamma",
    start = list(shape = 1, rate = 1)
  )

summary(fit)

## Fitting of the distribution ' gamma ' By maximum likelihood on censored data 
## Parameters
##        estimate Std. Error
## shape 2.9607131 0.13487956
## rate  0.7788964 0.03808087
## Loglikelihood:  -2111.847   AIC:  4227.693   BIC:  4237.509 
## Correlation matrix:
##           shape      rate
## shape 1.0000000 0.9253887
## rate  0.9253887 1.0000000

We see that the naive model has fit poorly due to the primary censoring and right truncation in the data.

4 Fitting an improved model using `primarycensored` and `fitdistrplus`

We’ll now fit an improved model using the primarycensored package. There are two approaches:

Recommended: Use fitdistdoublecens() - a convenience wrapper that handles all the complexity for you
Advanced/Educational: Define custom distribution functions manually (shown first for understanding)

4.1 Understanding the approach (advanced)

This section shows how to manually define custom distribution functions. You don’t need to do this yourself - fitdistdoublecens() handles it automatically. This is included to help you understand what’s happening under the hood.

To fit using fitdistrplus, we need to define custom distribution functions that account for primary censoring and truncation. Rather than using fitdistcens we use fitdist because our functions are handling the censoring themselves. Note that in this custom implementation for simplicity we are filtering to use only data with the same obs_time rather than handling varying observation times. This means we’re using a subset of our simulated data for the estimation.

# Define custom distribution functions using primarycensored
# The try catch is required by fitdistrplus
dpcens_gamma <- function(x, shape, rate) {
  result <- tryCatch(
    {
      dprimarycensored(
        x, pgamma,
        shape = shape, rate = rate,
        pwindow = 1, swindow = 1, D = 8
      )
    },
    error = function(e) {
      rep(NaN, length(x))
    }
  )
  return(result)
}

ppcens_gamma <- function(q, shape, rate) {
  result <- tryCatch(
    {
      pprimarycensored(
        q, pgamma,
        shape = shape, rate = rate,
        dpwindow = 1, D = 8
      )
    },
    error = function(e) {
      rep(NaN, length(q))
    }
  )
  return(result)
}

# Fit the model using fitdistcens with custom gamma distribution
pcens_fit <- delay_data |>
  dplyr::filter(relative_obs_time == 8) |>
  dplyr::pull(delay) |>
  fitdist(
    distr = "pcens_gamma",
    start = list(shape = 1, rate = 1)
  )

summary(pcens_fit)

## Fitting of the distribution ' pcens_gamma ' by maximum likelihood 
## Parameters : 
##        estimate Std. Error
## shape 1.7522811 0.19551646
## rate  0.4734692 0.08187069
## Loglikelihood:  -639.2144   AIC:  1282.429   BIC:  1290.003 
## Correlation matrix:
##           shape      rate
## shape 1.0000000 0.9266603
## rate  0.9266603 1.0000000

We see good agreement between the true and estimated parameters but with higher standard errors due to using a subset of the data.

4.2 Using `fitdistdoublecens()` (recommended)

Rather than defining custom functions manually, primarycensored provides the fitdistdoublecens() wrapper function that handles everything automatically. This is the recommended approach for most users.

Key advantages of fitdistdoublecens(): - No custom functions needed: Just specify the distribution name (e.g., "gamma", "lnorm", "weibull") - Handles varying observation windows: Supports different truncation times (D) and primary windows (pwindow) across observations - Familiar interface: Uses column names similar to fitdistcens() (left and right for censoring bounds) - Supports mixed censoring intervals: Different secondary censoring windows across observations are handled automatically

fitdistdoublecens_fit <- fitdistdoublecens(
  delay_data,
  distr = "gamma",
  start = list(shape = 1, rate = 1),
  left = "delay",
  right = "delay_upper",
  pwindow = "pwindow",
  D = "relative_obs_time"
)

summary(fitdistdoublecens_fit)

## Fitting of the distribution ' pcens_dist ' by maximum likelihood 
## Parameters : 
##        estimate Std. Error
## shape 1.6863057 0.10294344
## rate  0.4213108 0.03945095
## Loglikelihood:  -2064.778   AIC:  4133.556   BIC:  4143.371 
## Correlation matrix:
##           shape      rate
## shape 1.0000000 0.9196305
## rate  0.9196305 1.0000000

4.3 Summary

In this vignette we have shown how to fit a distribution using primarycensored in conjunction with fitdistrplus. The key takeaways are:

Use fitdistdoublecens(): This is the recommended approach for most users. It handles all the complexity of primary censoring, secondary censoring, and truncation automatically.
Specify distributions by name: Pass the base distribution name (e.g., "gamma", "lnorm", "weibull") to the distr parameter. The function automatically finds the corresponding d and p functions.
Ignoring censoring causes bias: The naive model that ignores primary censoring and truncation substantially underestimates the true distribution parameters.

For a more robust Bayesian approach to fitting distributions, see the vignette("fitting-dists-with-stan") vignette. For more flexible delay distribution fitting, see the epidist package (which uses primarycensored under the hood).

4.4 How you might adapt this vignette

This vignette uses simulated data, but you can adapt it for your own work:

Replace simulation with real data: Swap out the simulated delay_data with your own observations of delays between primary and secondary events
Change the distribution: Replace "gamma" with other distributions like "lnorm", "weibull", or "norm" depending on what fits your data
Vary the censoring windows: Adjust pwindow and swindow to match your data’s actual primary and secondary censoring intervals
Handle different truncation times: Use varying values in the D column if your observations have different maximum observable delays